Dreiecksrätsel mit Zauberquadrat (inkl. Lösung)
Im Internet kursiert ein interessantes Rätsel. Es geht um ein Dreieck, dass in vier Flächen eingeteilt ist: zwei Dreiecke und zwei L-förmige Rechtecke. Durch Verschieben der vier Flächen entsteht ein neues Dreieck, dass offensicht exakt gleich groß ist (wenn man die Kästchen abzählt). Aber: unten ist ein Quadrat über!? Die Frage lautet: "How can this be true?" - also: "Wie kann das sein?" (Lösung unten...).
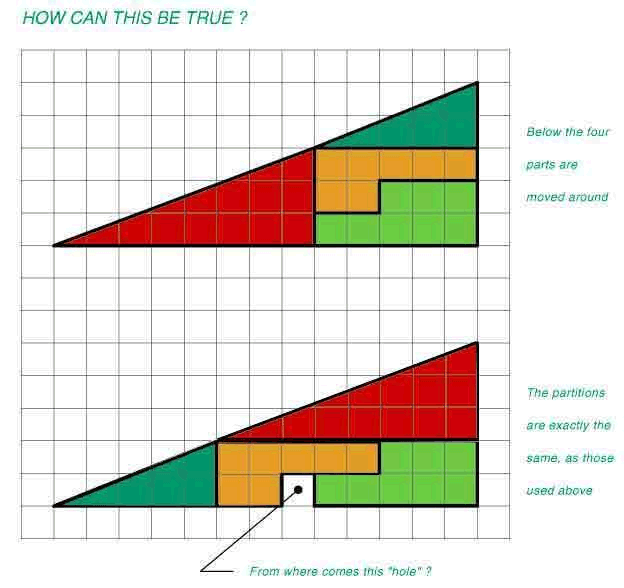
Im englischen wird dieses Rätsel das "Missing-Square-Puzzle" genannt, zu Deutsch: "Fehlendes-Quadrat-Rätsel". Erfunden hat es (vermutlich) der amerikanische Amateur-Magier Paul Curry (1917–1986), der aber vor allem durch eine Reihe von Kartenkunststücken berühmt wurde (z.B. "Out of this world"). Aber zurück zum Dreiecksrätsel...
Lösung ermitteln ...
Wenn man die Zeichnung genauer betrachtet, fallen allerdings die etwas dicken schwarzen Konturen der Formen auf. Und tatsächlich: wenn man diese Zeichnung mal sauber nachzeichnet, dann bemerkt man, dass der Schnittpunkt der Mittel-Horizontalen mit der Hypotenuse des Gesamt-Dreiecks nicht wirklich passt.
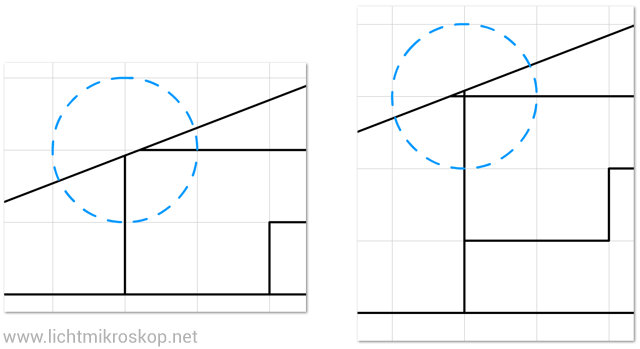
Und damit hat man auch schon fast die Lösung. Denn wenn man die Dreiecke korrekt konstuieren würde, dann wäre die Hypotenuse keine durchgehende gerade Linie, sondern hätte eine Delle in der Mitte. Im oberen Bild des Rätsels wäre die Ecke etwas außerhalb, so dass der Flächeninhalt der beide Dreiecke etwas größer wäre. Im unteren Bild des Rätsels liegt der Eckpunkt etwas innerhalb des Gesamtdreiecks, so dass der Flächeninhalt der beiden Dreiecke kleiner ist als zuvor.
Lösung
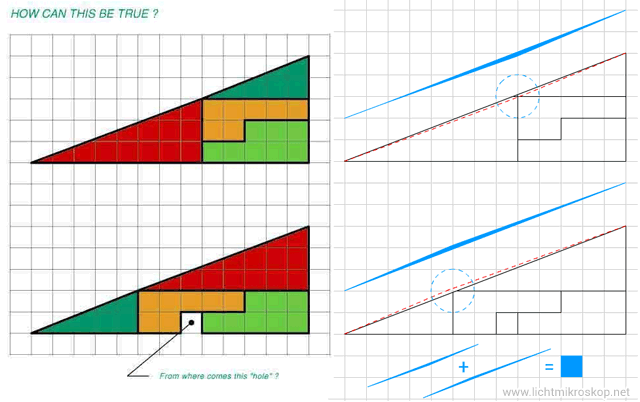
Wenn man die Differenz addiert - oben zu viel Flächeninhalt der Dreiecke und unten zu wenig Flächeninhalt, dann ergibt die Summe exakt den Flächeninhalt des kleinen, scheinbar hinzugezauberten Quadrats.
Was lernt man daraus? -> Immer schön sauber arbeiten, denn sonst kommt ein Ergebnis heraus, das richtig scheint, obwohl es falsch ist.
Praktisch beim Schokolade-Teilen ...
Wenn man das so anschaut und durchzählt, ist man wirklich geneigt zu glauben, als sei hier aus dem Nichts wie von Geisterhand ein zusätzliches Quadrat entstanden. Magisch und praktisch, vor allem, wenn man es mit einer Tafel Schokolade macht ...
Hier noch mal die Lösung in größerer Auflösung:
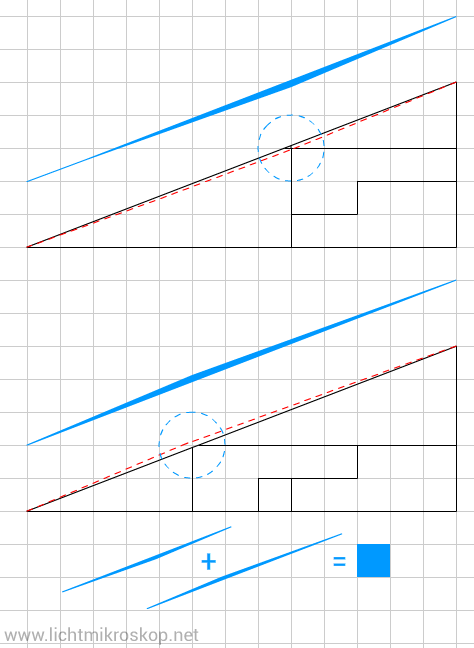
Alle Grafiken dieser Seite sind CreativeCommons CC-BY-SA. Sie können gerne (auch ohne Nachfrage) im Unterricht gezeigt und genutzt werden.
